Basic Concepts
Fourier transform
Given a signal $x(t)$, its Fourier transform is $$ \hat{x}(f) = \int_{-\infty}^{\infty}\exp(-i2\pi ft)x(t)dt. \tag{1} $$
Power spectral density (spectral line shape)
The power spectral density of a signal describes the distribution of power into frequency components. The calculation of power spectral should involve the calculation of Fourier transform. However, for a signal associated with a stationary process, its Fourier transform may diverge. Having said that, we can still define the power spectral density of a stationary-process signal.
The average power of singal $x(t)$ is $$ P = \lim_{T\rightarrow\infty}\frac{1}{T}\int_{t_{0}-T/2}^{t_{0}+T/2}|x(t)|^{2}dt, $$ where $t_{0}$ is an arbitrary time. We can write this expression of signal power in an alternative way. Let $x_{T}(t) = x(t)\omega_{T}(t)$, where $\omega_{T}(t)$ is unity within the length-T time frame and zero elsewhere. Then $$ P = \lim_{T\rightarrow\infty}\frac{1}{T}\int_{-\infty}^{\infty}|x_{T}(t)|^{2}dt. $$
Parseval’s theorem tells us that
$$ P = \lim_{T\rightarrow\infty}\frac{1}{T}\int_{-\infty}^{\infty}|\hat{x}_{T}(f)|^{2}df $$
$$ = \int_{-\infty}^{\infty}\lim_{T\rightarrow\infty}\frac{1}{T}|\hat{x}_{T}(f)|^{2}df. $$
Then the power spectral density is simply defined as the integrad above (see 1). $$ S_{xx}(f) = \lim_{T\rightarrow\infty}\frac{1}{T}|\hat{x}_{T}(f)|^{2}. \tag{2} $$
Phase noise
Here we focus on a specific type of signal - the laser output. A real laser must suffer from instaneous phase fluctuation $\delta\phi(t)$. The phase noise is commonly represented by its power spectral density, denoted as $S_{\phi}(f)$.
Frequency noise
When a laser has a fluctuation phase, its frequency will become unstable and fluctuate accordingly. The frequency fluctuation is $$ \delta\nu(t) = \frac{1}{2\pi}\frac{d\phi}{dt}. $$
In fact, phase noise and frequency noise are esentially referring to the same thing, i.e., the instantaneous phase fluctuation of laser. The frequency noise is usually characterized by its power spectral density, denoted as $S_{\nu}(f)$. There is a simple relation between $S_{\phi}(f)$ and $S_{\nu}(f)$ (see 2): $$ S_{\phi}(f) = \frac{S_{\nu}(f)}{f^{2}}. \tag{3} $$
As a consequence of the phase fluctuation, the power spectral density of the laser will deviate from an ideal delta function. Instead, it will manifest as a spectral line with a finite width. The full width half maximum (FWHM) of this spectral line is defined as the linewidth of the laser.
There is a simple relation between the laser linewidth $\Delta\nu_{\rm int}$, frequency noise power spectral density $S_{\nu}(f)$, and phase noise power spectral density $S_{\phi}(f)$ (see 2): $$ \int_{\Delta\nu_{\rm int}}^{\infty}S_{\phi}(f)df = \int_{\Delta\nu_{\rm int}}^{\infty}\frac{S_{\nu}(f)}{f^{2}}df = \frac{1}{\pi}\mathrm{rad}^{2}. \tag{4} $$
Noise sources
Laser output typically stems from two main sources: white noise and flicker (1/f) noise, as detailed in 3. White noise is a result of spontaneous emission, while flicker noise arises from fluctuations in various sources like the laser cavity and driver circuit. In terms of frequency noise power spectral density, white noise appears as a horizontal level, while flicker noise is evident as a 1/f section located on the low-frequency side.
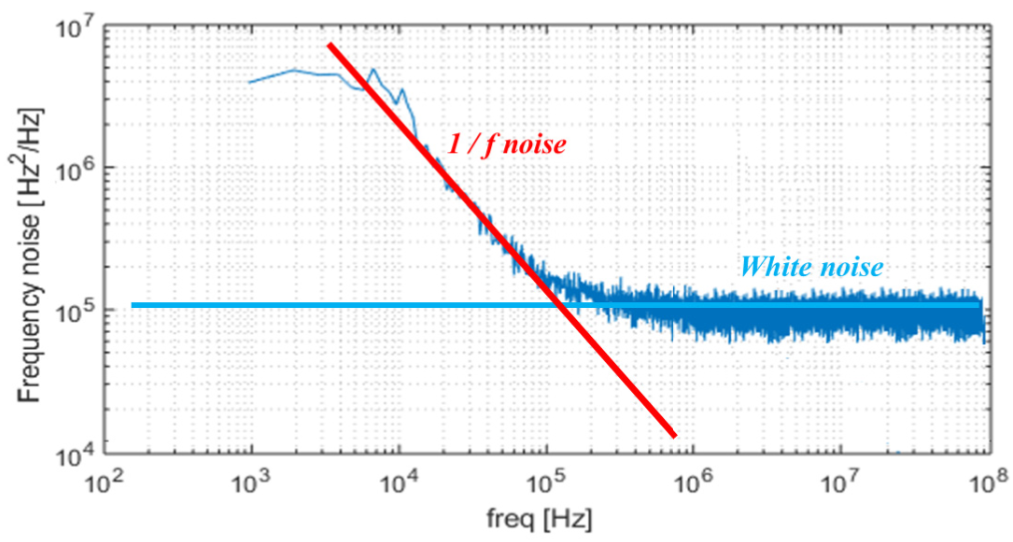
Usually, people presents the so-called fundamental/inherent/Schawlow-Townes/quantum-noise-limited Lorentzian linewidth in literature 4, which is simply $\pi$ times the white noise intensity. This linewidth should be distinguished from the FWHM of the spectral lineshape. The FWHM of the spectral lineshape is defined as integrated linewidth, which takes into account both the white noise (quantum noise) and 1/f noise (electric noise) and is thus always larger than the fundamental noise.
Relative intensity noise
Relative Intensity Noise (RIN) characterizes the fluctuations in the power level of a laser. This term is crucial in explaining lasers utilized in fiber-optic communication and LIDAR remote sensing. Unlike frequency noise or laser linewidth, which relies on the laser output’s phase, RIN solely relies on its amplitude. RIN is typically measured in units of dB/Hz. For instance, when the laser output undergoes an abrupt phase shift of π, it impacts the frequency noise or laser linewidth, but it does not alter the RIN.
References
- https://en.wikipedia.org/wiki/Spectral_density
- Tran, M. A., Huang, D., & Bowers, J. E. (2019). Tutorial on narrow linewidth tunable semiconductor lasers using Si/III-V heterogeneous integration. APL photonics, 4(11).
- https://emcore.com/wp-content/uploads/2021/04/EMCORE-Laser-Linewidth-Frequency-Noise-and-Measurement.pdf
- Tran, M. A., Huang, D., Guo, J., Komljenovic, T., Morton, P. A., & Bowers, J. E. (2019). Ring-resonator based widely-tunable narrow-linewidth Si/InP integrated lasers. IEEE Journal of Selected Topics in Quantum Electronics, 26(2), 1-14.