Introduction
Ring resonators are a fundamental component in integrated photonic circuits, serving as compact and narrow-band optical filters used in lasers, modulators, and (de-)multiplexers. There are two common configurations for how ring resonators interact with bus waveguides: the all-pass ring and add-drop ring configurations, illustrated in Figure 1. In the all-pass ring setup, the bus waveguide is evanescently coupled to the ring resonator, selectively tapping and dissipating pump light at resonant frequencies while allowing other optical signals to pass through with minimal loss. On the other hand, the add-drop ring configuration transfers pump light at resonant frequencies from the lower waveguide to the upper waveguide, avoiding dissipation within the ring. This note provides a theoretical analysis of the transmission properties of the all-pass ring using coupled mode theory.
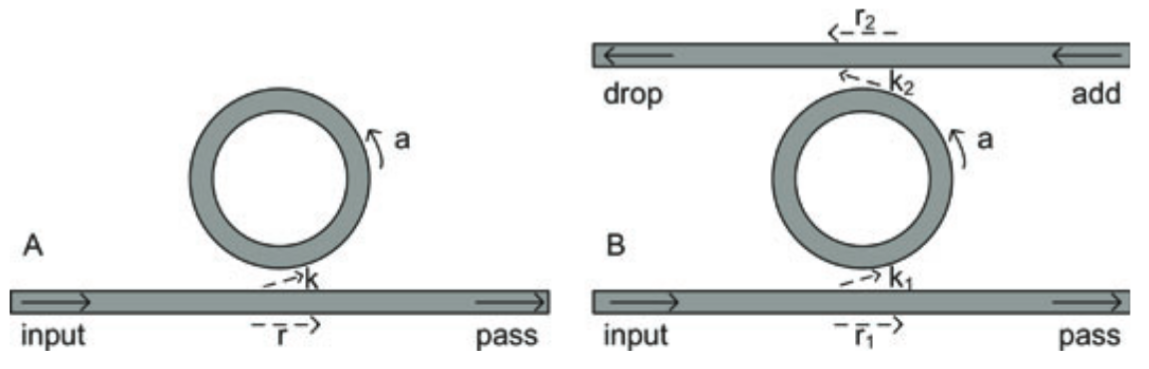
Left: all-pass ring; Right: add-drop ring [1].
Coupled Mode Theory of Ring Resonator
Transmittance of all-pass ring
In the all-pass ring configuration shown in Figure 1 (left), we define the roundtrip amplitude attenuation as $a$ and the amplitude self-coupling coefficient as $r$. Specifically, light circulating the ring over one cycle experiences an intensity attenuation of $a^{2} = e^{-\alpha L}$ due to intrinsic loss (such as scattering and radiation), where $\alpha$ is the attenuation coefficient and $L$ is the ring circumference. Moreover, the power coupling ratio between the ring and the bus waveguide is given by $|k|^{2} = 1 - |r|^{2}$, where $r = \cos(\kappa l)$ and $k = -j\sin(\kappa l)$ represent the amplitude self- and cross-coupling coefficients. Here, $\kappa$ and $l$ denote the coupling strength and length of the coupling region, respectively. It is important to note that there is a phase difference of $\pi/2$ between $k$ and $r; the derivation of this phase factor can be found in section 4.1 of the reference [1].
The amplitude of the transmitted field is directly proportional to the input field amplitude, with the ratio given by reference [1]:
$$ \frac{E_{\rm pass}}{E_{\rm input}} = r + k^{2}(ae^{-i\phi} + a^{2}re^{-i2\phi} + a^{3}r^{2}e^{-i3\phi} + …)\ = \frac{r-ae^{-i\phi}}{1-are^{-i\phi}}. \tag{1} $$
where $\phi = \beta L$ is the roundtrip phase shift, with $beta$ the propagation constant of the ring.
By taking the squared absoute value for both sides of Equation 1, we obtain the transmittance of the all-pass ring as follows:
$$ T = |\frac{E_{\rm pass}}{E_{\rm input}}|^{2} = \frac{a^{2} - 2ar\cos\phi + r^{2}}{1 - 2ar\cos\phi + (ar)^{2}}. \tag{2} $$
To make the frequency dependence of the all-pass ring transmittance clearer, we recast Equation 2 into
$$ T = 1 - \frac{(1-a^{2})(1-r^{2})}{1-2ar\cos\phi+(ar)^{2}}. \tag{3} $$
Since $0 < a, r < 1$, the all-pass ring transmittance exhibits local minima at $\phi = 2N\pi$ ($N = 1, 2, …$). These minima correspond to dips in the transmittance spectrum occurring at frequencies $f = N \times c/n_{\rm eff}L$, where $n_{\rm eff}$ represents the mode effective index. These dips coincide with the resonant frequencies of the ring resonator and are commonly referred to as resonance dips.
The free spectral range (FSR) of the ring resonator around the wavelength $\lambda$, which is defined as the spectral separation between the two nearest resonant wavelengths, is given by
$$ {\rm FSR}_{f} = \frac{c}{n_gL}. $$
Here, $n_{g} = n_{\rm eff} - \lambda dn_{\rm eff}/d\lambda$ denotes the group index of the ring at the wavelength $\lambda$.
Lorentzian line shape and Q factor
The fineness is determined by the ratio of the FSR to the FWHM of the resonance dip, also known as the resonance width. When the ring exhibits a fineness significantly greater than 1, the resonance width corresponds to a minimal variation in the roundtrip phase shift $\phi$ compared to $2\pi$. Under these conditions, the shape of the resonance dip can be approximated by a Taylor expansion of the all-pass ring transmittance around the resonant frequency $\omega$:
$$ T = 1 - \frac{(1-a^{2})(1-r^{2})}{(1-ar)^{2}+ar(\Delta\omega t_{\rm rt})^{2}}\ = 1 - \frac{h}{1 + (\frac{\Delta\omega}{w/2})^{2}}, \tag{4} $$
where $\Delta\omega$ represents the detuning from the resonant frequency, $t_{rt} = n_{g}L/c$ denotes the roundtrip time, $h = \frac{(1-a^{2})(1-r^{2})}{(1-ar)^{2}}$ denotes the resonance dip depth, $w = 2\frac{1-ar}{\sqrt{ar}}\frac{c}{n_{g}L}$ stands for the dip FWHM, and $n_{g} = n_{\rm eff}+f\frac{dn_{\rm eff}}{df} = n_{\rm eff}-\lambda\frac{dn_{\rm eff}}{d\lambda}$ is the group index. The minimum transmittance is $T_{\rm min} = T(\Delta\omega = 0) = \frac{(r-a)^{2}}{(1-ra)^{2}}$.
It is important to note that a Taylor expansion was applied around a resonant frequency. As the frequency of maximum transmittance for an all-pass ring is situated outside any resonant dip, away from any resonant frequency, the Taylor expansion cannot be utilized for calculating the maximum transmittance. Instead, Equation 3 should be employed to determine the maximum transmittance by setting $\phi = (2N+1)\pi$ for some non-negative integer $N$. The resulting transmittance is $T_{\rm max} = \frac{(r+a)^{2}}{(1+ra)^{2}}$ [2]. In summary, the FWHM and extinction ratio for a resonance dip of an all-pass ring can be obtained as follows:
$$ {\rm FWHM}_{\omega} = w = 2\frac{1-ar}{\sqrt{ar}}\frac{c}{n_gL}, \tag{5.1} $$
$$ {\rm ER} = \frac{T_{\max}}{T_{\min}} = \frac{(r+a)^{2}(1-ra)^{2}}{(1+ra)^{2}(r-a)^{2}}. \tag{5.2} $$
Importantly, $1 - T = h/[1+(\Delta\omega/(w/2))^{2}]$ describes a standard Lorentzian line shape with a height of $h$ and a full width at half maximum (FWHM) of $w$. Through Fourier transform, it can be demonstrated that this frequency-domain Lorentzian resonance dip corresponds to an exponentially decaying time-domain signal $s(t) \propto \exp(-wt/2-i\omega t)$, depicting a typical damped oscillation. This time-domain signal actually illustrates the evolution of the intracavity optical field amplitude, where the intracavity power $P \propto |s(t)|^{2} = \exp(-wt)$. Consequently, the FWHM of the resonance dip in the transmittance spectrum (power transmission versus angular frequency) is equivalent to the intracavity power decaying rate $|\frac{1}{P}\frac{dP}{dt}| = w$.
In general terms, the attenuation rate of a damped oscillation is quantified by the Q factor, defined as $Q = \omega/w = 2\pi\tau/T$, where $w$ signifies the power attenuation rate, $\omega$ represents the oscillation angular frequency, $\tau = 1/w$ denotes the decay time, and $T = 2\pi/\omega$ indicates the oscillation period. For a ring resonator coupled (or loaded) to a bus waveguide, both the intrinsic loss $a$ and the coupling loss $r$ contribute to $\omega$ and hence determine $Q$. In this scenario, the Q factor is termed as the loaded Q factor. As the coupling strength between the ring and the bus waveguide decreases, the loaded Q factor of the ring will approach a value determined by the intrinsic loss. This specific value is called the intrinsic Q factor, which is computed by assuming no coupling loss ($r = 1$).
The PDF version of this note is available here.
Reference
- Okamoto, K. (2010). Fundamentals of optical waveguides. Elsevier.
- Bogaerts, W., De Heyn, P., Van Vaerenbergh, T., De Vos, K., Kumar Selvaraja, S., Claes, T., … & Baets, R. (2012). Silicon microring resonators. Laser & Photonics Reviews, 6(1), 47-73.