Note on Attention Mechanism

Introduction

Attention mechanism is one fundamental building component in modern natural language processing systems like Transformer and GPT-3. These systems employ the encoder-decoder architecture, where the encoder maps input sentences to a fixed-length vector, which is then transformed to output sentences by the decoder. This architecture suffers from performance degradation when it comes to long input sentences. Fortunately, this issue can be effectively mitigated by employing the attention mechanism, which identifies the relevant part of the input sentence for the encoder to map, making the problematic mapping from the whole input sentence to a fixed-length vector unnecessary.

The attention mechanism was first proposed in [1] by Bahdanau, D. et. al., where it was implemented as part of an RNN Encoder-Decoder architecture. This neural network model demonstrated state-of-the-art performance in English-to-French translation and was published in ICLR 2015. As of 2024, this paper has been cited more than 30,000 times.

The RNN Encoder-Decoder model consists of two RNNs serving as the encoder and the decoder, respectively. The encoder RNN maps input words $x_{j}$ to a series of hidden states $h_{j}$ ($j = 1, 2, …, T_{x}$). Then, these hidden states are used to determine a context vector $c_{i}$ for predicting the $i$-th target word. That is to say, the decoder RNN uses its last hidden state $s_{i-1}$, last target word $y_{i-1}$, and the current context vector $c_{i}$ as input for predicting the $i$-th target word.

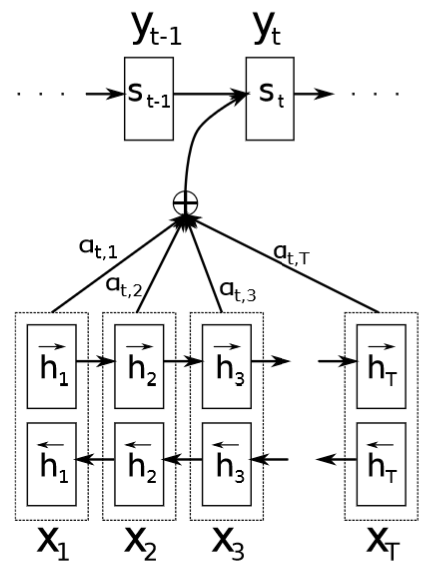
Fig. 1 Diagram of attention mechanism in an RNN encoder-decoder architecture [1]

The key idea of the attention mechanism lies in the definition of the context vector $c_{i}$. The context vector is defined as a weighted sum of all these hidden states:

$$ c_{i} = \sum_{j=1}^{T_{x}}\alpha_{ij}h_{j}, $$

where the coefficients $\alpha_{ij}$ quantify the relevance of each source word $x_{j}$ to the $i$-th target word. These coefficients are calculated as a softmax function as follows:

$$ \alpha_{ij} = \frac{\exp(e_{ij})}{\sum_{j=1}^{T_{x}}\exp(e_{ij})}, $$

where $e_{ij} = a(s_{i-1}, h_{j})$. The function $a$ is a feedforward neural network to be jointly trained with the RNNs, which serves the purpose of predicting the relevance of each source word for generating the next target word. Intuitively, for a long source sentence, most source words will be assigned with low weights. This effectively avoids the issue of mapping the entire sentence to a fixed-length vector, resulting in a significant performance improvement of the model for handling long input sentences.

It is worth mentioning that since the weights $\alpha_{ij}$ quantify the relevance between source words and target words, they can be used for alignment. This observation explains the title of this paper: “Neural machine translation by jointly learning to align and translate.”

Reference

1. Bahdanau, D., Cho, K., & Bengio, Y. (2014). Neural machine translation by jointly learning to align and translate. arXiv preprint arXiv:1409.0473.
2. Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., & Bengio, Y. (2014). Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv preprint arXiv:1406.1078.
3. Sutskever, I., Vinyals, O., & Le, Q. V. (2014). Sequence to sequence learning with neural networks. Advances in neural information processing systems, 27.