Note on Effective Index

Introduction

When light travels through a waveguide, its phase undergoes periodic changes as it moves along. The effective index is a measure of how frequently these phase changes occur compared to the wavelength of light in free space, but with the same frequency. Mathematically, the effective index, denoted as $n_{\rm eff}$, is defined as [1]:

$$ n_{\rm eff} = \frac{\lambda}{2\pi}\beta = \frac{\beta}{k}, $$

where $\beta$ represents the propagation constant of a specific mode in the waveguide. It’s important to note that different modes in the waveguide have distinct effective index values, meaning $n_{\rm eff}$ is a function of the mode index.

Effective Index of Slab Waveguide

A slab waveguide refers to a two-dimensional layer with a high refractive index, positioned between two layers with lower refractive indices. This heterogenous structure allows for the emergence of confined optical modes within the middle layer, effectively creating an optical waveguide. In the case where both the upper and bottom layers are composed of the same material, we classify this type of waveguide as symmetric.

The effective index of confined modes in a symmetric slab waveguide can be determined through analytical calculations. Below we will focus on TE modes only for simplicity. In this case, we denote the refractive index of the middle layer as $n_{1}$ and the refractive index of the upper and lower layers as $n_{s}$. For a slab waveguide with a core thickness of $2a$, the effective index $n_{\rm eff}$ can be calculated using the equation provided on page 19 in reference [2]:

$$ v\sqrt{1-b} = \frac{m\pi}{2} + \tan^{-1}\sqrt{\frac{b}{1-b}}, $$

where $v = ka\sqrt{n_{1}^{2}-n_{s}^{2}}$ and $b = (n_{\rm eff}^{2} - n_{s}^{2})/(n_{1}^{2} - n_{s}^{2})$. $m$ is a nonnegative integer and represents the mode index.

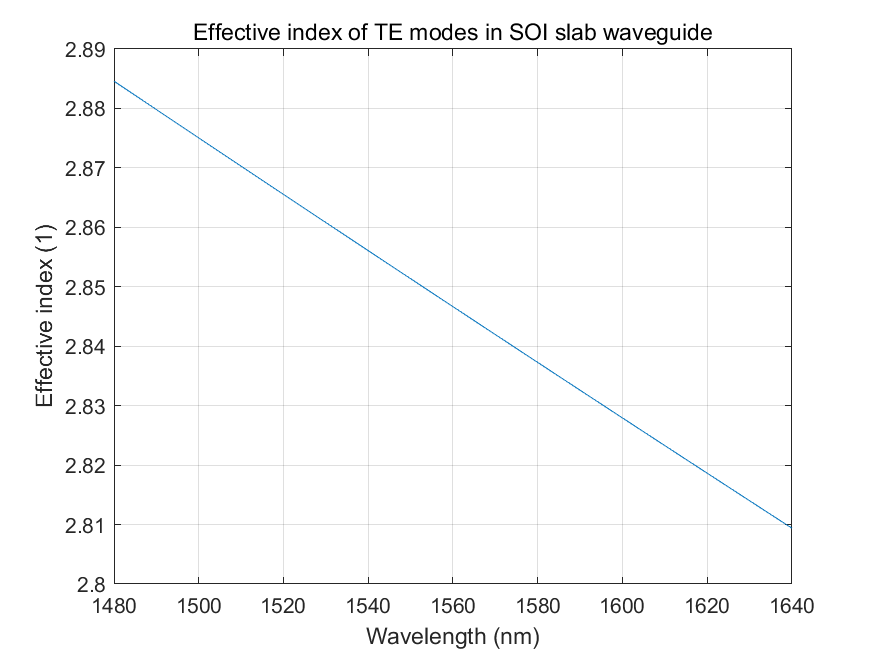
Here, we present the dispersion curves for the first TE mode in a slab waveguide. The waveguide consists of a 220-nanometer-thick silicon layer at the center, with silicon dioxide layers positioned above and below it.

Code

My MATLAB code for analytically calculating effective index of symmetric slab waveguide can be found at Note_effective_index/effective_index_slab_wg.m.

References

1. https://www.rp-photonics.com/effective_refractive_index.html
2. Okamoto, K. (2021). Fundamentals of optical waveguides. Elsevier.